대표적인 정렬 알고리즘 몇 가지를 정리해 보려고 한다.
참고로 시간 복잡도의 빠르기는 다음과 같다.



선택정렬(Selection Sort)
주어진 배열에서 가장 작은 값을 찾아 첫 번째 원소와 교환하고, 그 다음으로 작은 값을 두 번째 원소와 교환하는 방식으로 정렬을 수행.
ex) 9,6,7,3,5가 들어있는 배열을 선택정렬방식으로 정렬하기

장점
- 구현이 간단하다.
- 비교횟수는 많지만 교환 횟수가 적어서 많은 교환이 일어나야 하는 자료상태에서 효율적으로 사용할 수 있다.
- 버블 정렬과 마찬가지고 O(n^2)의 시간복잡도를 갖지만 실제로는 버블정렬보다 조금 더 빠르다.
단점
- 항상 O(n^2)의 시간복잡도를 가지기 때문에 오래걸린다.
시간 복잡도
- 최선, 최악, 평균 모두 O(n^2)이다.
삽입정렬(Insertion Sort)
처음 key 값은 배열의 두 번째 자료부터 시작하며, key와 그 앞의 자료들과 비교하여 삽입할 위치를 지정한 후 지정한 위치에 자료를 삽입하여 정렬한다.
ex) 8, 5, 6, 2, 4가 들어있는 자료를 삽입정렬

장점
- 배열이 거의 정렬되어 있는 상태라면 최선의 경우 O(n)으로 빠르다.
- 보통의 경우 퀵 정렬이 더 효율적이지만 거의 정렬되어 있는 상태라면 퀵 정렬보다 강력하다.
단점
- 최악의 경우 O(n^2)으로 데이터의 크기 및 상태에 따라 성능의 편차가 심하다.
시간 복잡도
- 최선 : O(n)
- 최악 : O(n^2)
- 평균 : O(n^2)
버블정렬(Bubble Sort)
배열의 첫 원소부터 시작하여 서로 인접한 두 원소를 검사하여 정렬한다.
ex) 7,4,5,1,3이 저장되어 있는 배열을 버블정렬

*한 회전이 끝날때마다 뒤에서부터 정렬이 완료된다.
장점
- 구현이 간단하다
단점
- 비효율적이다. (사실상 거의 쓰이지 않음)
시간 복잡도
- 최선, 최악, 평균 모두 O(n^2)
힙 정렬(Heap Sort)
완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
힙 자료구조를 사용하여 정렬을 수행하는 방식으로, 주어진 배열을 최대 힙 또는 최소 힙으로 구성한 후 힙에서 원소를 하나씩 꺼내 정렬한다.
ex)최대 힙에 새로운 요소 8 삽입

장점
- 시간 복잡도가 좋은 편
- 추가적인 메모리를 필요로 하지 않으면서 항상 O(nlogn)의 시간복잡도를 가진다.
- 힙 정렬이 유용한 경우는 전체 자료를 정렬하는 것이 아니라 가장 큰 값 몇개만 필요할 때!
단점
- 안정성을 보장받지 못한다.
시간 복잡도
- 최선, 최악, 평균 모두 O(nlogn)
병합(합병) 정렬(Merge Sort)
분할 정복 알고리즘의 하나(divide and conquer)로 하나의 리스트를 두개의 균등한 크기로 나누고, 분할된 부분 리스트를 정렬한 다음 두개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
ex) 21, 10, 12, 20, 25, 13, 15, 22를 병합정렬
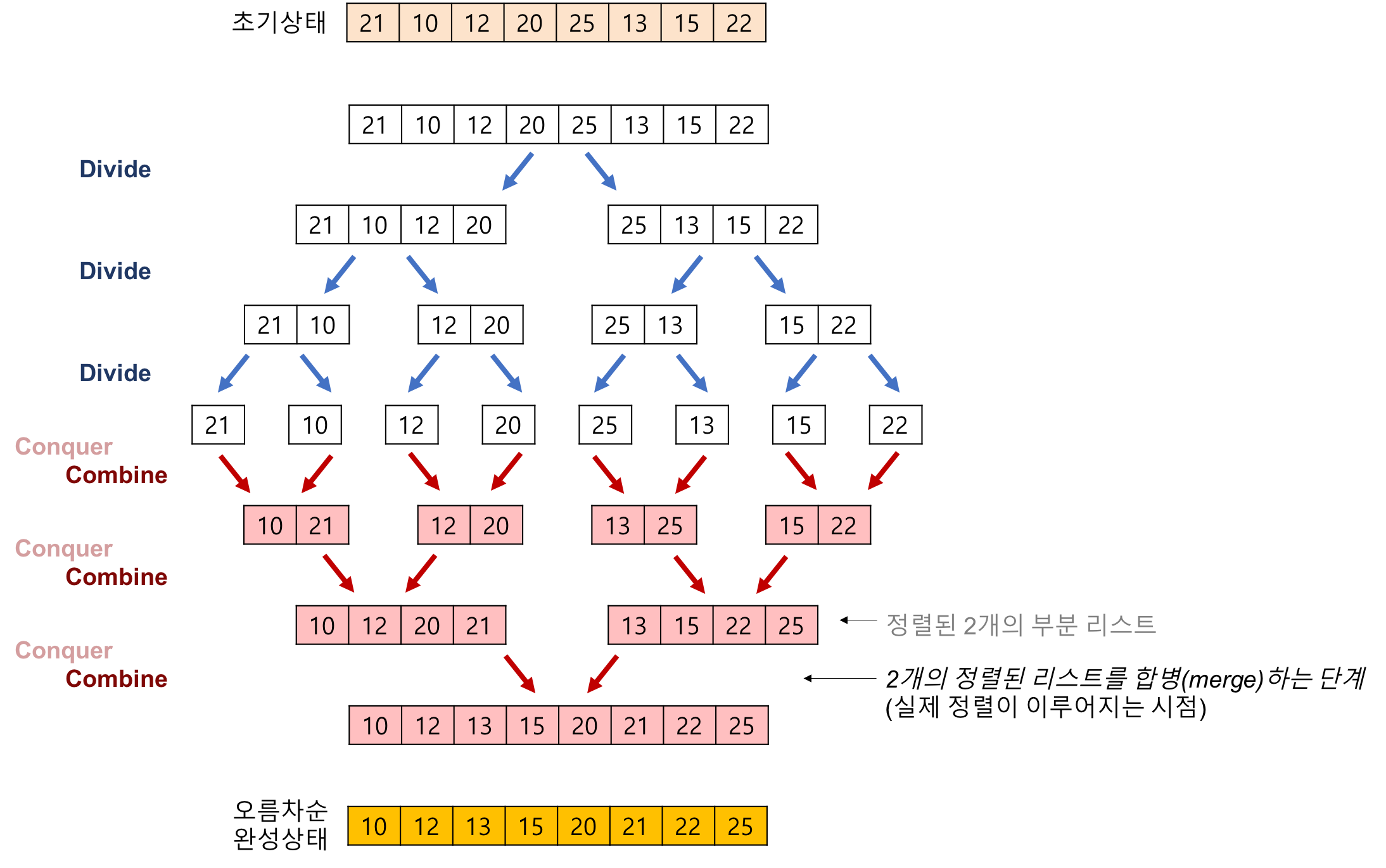
장점
- 데이터의 분포에 영향을 덜 받으며 안정적이다.
- 항상 O(nlogn)이라는 시간복잡도를 갖는다.
단점
- 추가적인 메모리가 필요하다.
- 데이터의 크기가 큰 경우 이동 횟수가 많아서 매우 큰 시간적 낭비를 초래한다.
시간 복잡도
- 최선, 최악, 평균 모두 O(nlogn)
퀵 정렬(Quick Sort)
병합 정렬과 마찬가지로 분할 정복(divide and conquer)알고리즘의 하나
1. 리스트 안에 한 요소를 선택한다 -> 이 원소가 피벗(pivot)
2. 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고, 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다.
3. 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.(부분 리스트 안에서도 다시 피벗을 정하고 피벗을 기준으로 부분 리스트로 나눈 후 정렬하는 과정 반복)
4. 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다. (리스트의 크기가 0이나 1이 될때까지 반복)
ex) 5, 3, 8, 4, 9, 1, 6, 2, 7을 퀵 정렬로 정렬

장점
- 실행시간이 O(nlogn)으로 준수한 편
단점
- pivot에 따라서 시간복잡도가 크게 달라지며 최악의 경우 O(n^2)라는 시간복잡도를 갖게 된다.
시간 복잡도
- 최선 : O(nlogn)
- 최악 : O(n^2)
- 평균 : O(nlogn)
정리
단순하지만 비효율적인 방법
- 삽입, 선택, 버블
복잡하지만 효율적인 방법
- 퀵, 힙, 병합, 기수



버블정렬은 왜 최선의 경우가 찾는 자료마다 다 다르지..?
'알고리즘' 카테고리의 다른 글
| 그리디 알고리즘(탐욕법, Greedy Algorithm) (1) | 2025.02.01 |
|---|---|
| 투 포인터(Two Pointers) (0) | 2025.01.12 |
| 이진 탐색(Binary Search) (1) | 2025.01.09 |